Kalkulus
Kalkulus (basa Latin: calculus, tegesé "watu cilik", kanggo ngétung) iku cabang èlmu matématika kang nyakup limit, turunan, integral, lan dhèrèt ora kakira étungané. Kalkulus iku èlmu ngenani owah-owahan, kaya déné géometri iku èlmu ngenani wangun lan aljabar iku èlmu ngenani panggarapkan kanggo mecahaké pepadhan sarta aplikasiné. Kalkulus dikembangké saka aljabar lan geometri. Kalkulus mligi nyinaoni kang ana gayutané karo laju utawa tingkat pagerakan, misalé percepatan, kurva, lan kamiringan. Kalkulus duwé aplikasi kang wiyar sajeroning babagan-babagan sains, ékonomi, lan tèhnik; sarta bisa mecahaké manéka masalah kang ora bisa dipecahaké mawa aljabar èlemèntèr.
Dhasar kalkulus yaiku turunan, integral, lan limit. Salah siji tujuan utama perkembangan kalkulus yaiku kanggo pamecahan masalah garis singgung.
Kalkulus duwé rong cabang utama, kalkulus diferensial lan kalkulus integral kang silih gegandhèngan liwat téoréma dhasar kalkulus. Pelajaran kalkulus iku lawang gerbang nuju wulangan matématika liyané kang luwih dhuwur, kang mirunggan nyinaoni fungsi lan limit, kang kanthi umum dijenengi analisis matématika.
Perkembangan kalkulus mligi dijurung déning Archimedes, Leibniz, Newton, Barrow, Descartes, de Fermat, Huygens, lan Wallis.
Sajarah[besut | besut sumber]


Perkembangan[besut | besut sumber]
Sajarah perkembangan kalkulus bisa dideleng ing sapérangan périodhe jaman, yaiku jaman kuna, jaman patengahan, lan jaman modhèren. Ing périodhe jaman kuna, sapérangan pamikiran ngenani kalkulus integral wis mijil, nanging ora dikembangaké kanthi becik lan sistematis. Pangétungan volume lan wiyar kang wujud fungsi utama saka kalkulus integral bisa ditlusuri manèh ing Papirus Moskwa Mesir (c. 1800 SM). Ing papirus mau, wong Mesir wis bisa ngétung volume piramida kapancung.[1] Archimedes ngembangaké pamikiran iki luwih adoh lan ngripta heuristik kang mèmper kalkulus integral.[2]
Nalika jaman patengahan, matématikawan India, Aryabhata, migunakaké konsèp cilik ora kaétung nalika taun 499 lan ngèksprèsikaké masalah astronomi sajeroning wangun pepadhan diferensial dhasar.[3] Pepadhan iki banjur ngeteraké Bhāskara II ing abad angka 12 kanggo ngembangaké wangun awal turunan kang makili owah-owahan kang cilik banget ora kaétung lan njelasaké wangun awal saka "Téoréma Rolle".[4] Watara taun 1000, matématikawan Irak Ibn al-Haytham (Alhazen) dadi wong pisanan kang ngedhunaké rumus pangétungan asil gunggung pangkat papat, lan kanthi migunakaké indhuksi matématika, panjenengané ngembangaké siji métodhe kanggo ngedhunaké rumus umum saka asil pangkat integral kang wigati banget marang perkembangan kalkulus integral.[5] Nalika abad angka 12, siji wong Pèrsi Sharaf al-Din al-Tusi nemu turunan saka fungsi kubik, siji asil kang wigati sajeroning kalkulus diferensial.[6] Nalika abad angka 14, Madhava, bebarengan karo matématikawan-astronom saka madahab astronomi lan matématika Kerala, njelasaké kasus mirunggan saka dhèrèt Taylor[7], kang ditulisaké sajeroning tèks Yuktibhasa.[8][9][10]
Ing jaman modhèren, panemon indhepèndhen dumadi nalika awal abad angka 17 ing Jepang déning matématikawan kaya déné Seki Kowa. Ing Éropah, sapérangan matématikawan kaya déné John Wallis lan Isaac Barrow mènèhaké terobosan sajeroning kalkulus. James Gregory mbuktèkaké siji kasus mirunggan saka téoréma dhasar kalkulus nalika taun 1668.
Leibniz lan Newton nyurung pamikiran-pamikiran iki bebarengan minangka siji kamanunggalan lan kaloro èlmuwan mau dianggep panemu kalkulus kanthi kapisah ing sajeroning wektu kang mèh bebarengan. Newton ngaplikasikaké kalkulus kanthi umum menyang babagan fisika sauntara Leibniz ngembangaké notasi-notasi kalkulus kang akèh dipigunakaké saiki.
Nalika Newton lan Leibniz mublikasikaké asilé kanggo sepisanané, mijil kontrovèrsi ing antarané matématikawan ngenani endi kang luwih patut kanggo nampa bebungah marang kerjané. Newton ngedhunaké asil kerjané luwih dhisik, nanging Leibniz kang pisanan mublikasikaké. Newton nutuh Leibniz nyolong pamikirané saka cathetan-cathetan kang ora dipublikasikaké, kang asring disilihaké Newton marang sapérangan anggota saka Royal Society.
Pamriksan kanthi princi nuduhaké yèn kaloroné nyambut gawé kanthi kapisah, kanthi Leibniz miwiti saka integral lan Newton saka turunan. Saiki, Newton lan Leibniz diwènèhi bebungah sajeroning ngembangaké kalkulus kanthi kapisah. Leibniz kang mènèhi jeneng marang èlmu cabang matématika iki minangka kalkulus, sauntara Newton njenengi "The science of fluxions".
Wiwit wektu iku, akèh matématikawan kang mènèhaké kontribusi marang pangembangan luwih lanjut saka kalkulus.
Kalkulus dadi topik kang umum banget ing SMA lan universitas jaman modhèren. Matématikawan saindhenging donya terus mènèhaké kontribusi marang perkembangan kalkulus.[11]
Prabawa wigati[besut | besut sumber]
Sanajan sapérangan konsèp kalkulus wis dikembangaké luwih dhisik ing Mesir, Yunani, Tiongkok, India, Iraq, Pèrsi, lan Jepang, panggunaaan kalkulus modhèren diwiwiti ing Éropah nalika abad angka 17 wektu Isaac Newton lan Gottfried Wilhelm Leibniz ngembangaké prinsip dhasar kalkulus. Asil kerjané banjur mènèhi prabawa kang kuwat marang perkembangan fisika.
Aplikasi kalkulus diferensial ngambah pangétungan karikatan lan percepatan, kamiringan siji kurva, lan optimalisasi. Aplikasi saka kalkulus integral ngambah pangétungan wiyar, volume, dawa busur, punjer massa, makarya, lan tekanan. Aplikasi luwih adoh ngambah dhèrèt pangkat lan dhèrèt Fourier.
Kalkulus uga kanggo éntuk pamahaman kang luwih rinci ngenani ruwang, wektu, lan obah (obah). Sakwéné maabad-abad, para matématikawan lan filsuf ngupaya mecahaké paradhoks kang ngambah pambagian wilangan karo nol utawa uga gunggung saka dhèrèt ora kaétung. Sawijining filsuf Yunani kuna mènèhaké sapérangan conto misuwur kaya déné paradhoks Zeno. Kalkulus mènèhaké solusi, mligi ing babagan limit lan dhèrèt ora kaétung, kang banjur kasil mecahaké paradhoks mau.
Prinsip-prinsip dhasar[besut | besut sumber]
Limit lan cilik ora kakira étungané[besut | besut sumber]

Kalkulus lumrahé dikembangaké kanthi manipulasi sapérangan kuantitas kang cilik banget. Objèk iki, kang bisa dilakokaké minangka angka, iku cilik banget. Sawijining wilangan dx kang ciliké ora kakira étungané bisa luwih gedhé tinimbang 0, nanging luwih cilik tinimbang wilangan apa waé ing dhèrèt 1, ½, ⅓,... lan wilangan réal positif apa waé. Saben pangepingan karo cilik ora kakira étungané (infinitesimal) tetepa cilik ora kakira étungané, mawa tembung liya cilik ora kakira étungané ora nyukupi properti Archimedes. Saka pandelengan iki, kalkulus iku sakumpulan tèhnik kanggo manipulasi cilik ora kakira étungané.
Nalika abad angka 19, konsèp cilik ora kakira étungané iki ditinggalaké amarga ora cukup tliti, suwaliké konsèp iki digantèkaké déning konsèp limit. Limit njelasaké pangaji siji fungsi ing pangaji input tinentu kanthi asil saka pangaji input paling cerak. Saka pandelengan iki, kalkulus iku sakumpulan tèhnik manipulasi limit-limit tinentu. Sacara tliti, dhéfinisi limit siji fungsi yaiku:
Diwènèhaké fungsi f(x) kang kadhéfinisikaké ing interval ing saubengé p, kajaba mungkin ing p iku dhéwé. Awaké dhéwé nelakaké yèn limit f(x) nalika x nyeraki p iku L, lan nulisaké:
yèn, kanggo saben wilangan ε > 0, ana wilangan δ > 0 kang silih korèspondhèn karo dhèwèké samengkono rupané kanggo saben x:
Turunan[besut | besut sumber]
Turunan saka siji fungsi makili owah-owahan kang cilik banget saka fungsi mau marang variabelé. Prosès nemu turunan saka siji fungsi diarani pandiferensialan utawa uga diferensiasi.
Sacara matématis, turunan fungsi ƒ(x) marang variabel x iku ƒ′ kang pangajiné ing titik x yaiku:
- ,
kanthi sarat limit mau èksis. Yèn ƒ′ èksis ing titik x tinentu, awaké dhéwé bisa nélakaké yèn ƒ kadiferensialaké (duwé turunan) ing x, lan yèn ƒ′ èksis ing saben titik ing domain ƒ, awaké dhéwé sebut ƒ kadiferensialaké.
Yèn z = x + h, h = x-z, lan h nyeraki 0 yèn lan mung yèn z nyeraki x, mula dhéfinisi turunan ing ndhuwur bisa uga ditulis minangka:
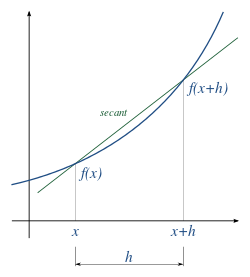
Gatèkna manawa èksprèsi ing dhéfinisi turunan ing ndhuwur wujud gradièn saka garis sekan kang ngliwati titik (x,ƒ(x)) lan (x+h,ƒ(x)) ing kurva ƒ(x). Manawa awaké dhéwé njupuk limit h nyeraki 0, mula awaké dhéwé bakal éntuk kamiringan saka garis singgung kang nyinggung kurva ƒ(x) ing titik x. Iki ateges uga garis singgung siji kurva wujud limit saka garis sekan, semono uga turunan saka siji fungsi ƒ(x) wujud gradièn saka fungsi mau.
Minangka conto, kanggo nemu gradièn saka fungsi ing titik (3,9):
Èlmu kang nyinaoni dhéfinisi, properti, lan aplikasi saka turunan utawa kamiringan saka siji grafik diarani kalkulus diferensial

Notasi pandhiferènsialan[besut | besut sumber]
Ana manéka jinis notasi matématika kang bisa kanggo nélakaké turunan, ngambah notasi Leibniz, notasi Lagrange, notasi Newton, lan notasi Euler.
Notasi Leibniz ditepungaké déning Gottfried Leibniz lan wujud salah siji notasi kang paling awal digunakaké. Iki asring digunakaké mligi nalika gegandhèngan antar y = ƒ(x) dideleng minangka gegandhèngan fungsional antarané variabel bébas karo variabel kaiket. Turunan saka fungsi mau marang x ditulis minangka:
- utawa uga
Notasi Lagrange ditepungaké déning Joseph Louis Lagrange lan wujud notasi kang paling asring digunakaké. Sajeroning notasi iki, turunan fungsi ƒ(x) ditulis minangka ƒ′(x) utawa uga mung ƒ′.
Notasi Newton, uga diarani notasi titik, mapanaké titik ing sandhuwuré fungsi kanggo nengeri turunan. Yèn y = ƒ(t), mula makili turunan y marang t. Notasi iki mèh kanthi èksklusif kanggo nglambangaké turunan marang wektu. Notasi iki asring katon sajeroning babagan fisika lan babagan matématika kang gegandhèngan karo fisika.
Notasi Euler migunakaké operator diferensial D kang ditrapaké ing fungsi ƒ kanggo mènèhaké turunan pisanané Df. Yèn y = ƒ(x) iku variabel kaiket, mula asring x dilekataké marang D kanggo nglarifikasikaké kabébasan variabel x. Notasi Euler banjur ditulis minangka:
- atau .
Notasi Euler iki asring digunakaké sajeroning ngrampungaké pepadhan diferensial linear.
| Notasi Leibniz | Notasi Lagrange | Notasi Newton | Notasi Euler | |
|---|---|---|---|---|
| Turunan ƒ(x) marang x | ƒ′(x) | kanthi y = ƒ(x) |
Integral[besut | besut sumber]

Integral wujud siji objèk matématika kang bisa diinterpretasikaké minangka wiyar wewengkon utawa uga generalisasi siji wewengkon. Prosès nemu integral siji fungsi diarani pangintegralan utawa uga integrasi. Integral dipérang dadi loro, yaiku: integral tinentu lan integral ora tentu. Notasi matématika kang kanggo nélakaké integral yaiku , kaya ta huruf S kang manjang (S singkatan saka "Sum" kang tegesé panggunggungan).
Integral tinentu[besut | besut sumber]
Diwènèhaké siji fungsi ƒ mawa variabel réal x lan interval antara [a, b] ing garis réal, integral tinentu:
kanthi informal didhèfinisikaké minangka wiyar wewengkon ing babagan xy kang diwatesi déning kurva grafik ƒ, sumbu-x, lan garis vèrtikal x = a lan x = b.
Ing notasi integral ing ndhuwur: a iku wates ngisor lan b iku wates ndhuwur kang nemtokaké domain pangintegralan, ƒ yaiku integran kang bakal diévaluasi marang x ing interval [a,b], lan dx wujud variabel pangintegralan.

Ana manéka jinis pandhefinisian formal integral tinentu, nanging kang paling umum digunakaké yaiku dhefinisi integral Riemann. Integral Rieman didhèfinisikaké minangka limit saka panggunggungan Riemann. Upamané awaké dhéwé arep golèk wiyar laladan kang diwatesi déning fungsi ƒ ing interval katutup [a,b]. Nalika nggolèki wiyar laladan mau, interval [a,b] bisa dipérang dadi akèh subinterval kang ambané ora kudu padha, lan awaké dhéwé milih sapérangan n-1 titik {x1, x2, x3,..., xn-1} antara a karo b saéngga njangkepi gegandhèngan:
Himpunan iku ingaran minangka partisi [a,b], kang mbagi [a,b] dadi sapérangan n subinterval . Amba subinterval pisanan [x0,x1] dinyatakaké minangka Δx1, mangkono uga amba subinterval angka i dinyatakaké minangka Δxi = xi-xi-1. Ing saben subinterval iki dipilih siji titik sembarang lan ing subinterval angka i mau dipilih titik sembarang ti. Mula ing saben subinterval bakal ana batangan pasagi dawa kang ambané Δx lan dhuwuré wiwit saka sumbu x tekan titik (ti, ƒ(ti)) ing kurva. Yèn awaké dhéwé ngétung wiyar saben batangan mau kanthi ngepingaké ƒ(ti)· Δxi lan nggunggungaké sakabèhing wiyar laladan batangan mau, awaké dhéwé bakal éntuk:
Panggunggungan Sp diarani panggunggungan Riemann kanggo ƒ ing interval [a,b]. Gatèkna yèn saya cilik subinterval partisi kang dijupuk, asil panggunggungan Riemann iki bakal saya nyeraki pangaji wiyar laladan kang dipénginaké. Yèn awaké dhéwé njupuk limit saka norma partisi nyeraki nol, mula awaké dhéwé bakal éntuk wiyar laladan mau.
Sacara tliti, dhéfinisi integral tinentu minangka limit saka panggunggungan Riemann yaiku:
Diwènèhaké ƒ(x) minangka fungsi kang kadhéfinisikaké ing interval katutup [a,b]. Ditélakaké yèn wilangan I iku integral tinentu ƒ ing sadawané [a,b] lan yèn I iku limit saka panggunggungan Riemann ing kaanan: Kanggo saben wilangan ε > 0 apa waé ana siji wilangan δ > 0 kang silih korèspondhènsi karo dhèwèké kanggo saben partisi ing sadawané [a,b] kanthi lan pilihan ti apa waé ing [xk-1, ti], awaké dhéwé éntuk
Sacara matématis bisa ditulisaké:
Yèn saben partisi duwé sapérangan n subinterval kang padha, mula amba Δx = (b-a)/n, saéngga pepadhan ing ndhuwur bisa uga ditulis minangka:
Limit iki mesthi dijupuk nalika norma partisi nyeraki nol lan gunggung subinterval kang ana nyraki ora kaétung akèhé.
- Conto
Minangka conto, yèn awaké dhéwé arep ngétung integral tinentu , yaiku golèk wiyar laladan A ing sangisoré kurva y=x ing interval [0,b], b>0, mula pangétungan integral tinentu minangka limit saka panggunggungan Riemanné yaiku
Pamilihan partisi utawa titik ti kanthi sembarang bakal ngasilaké pangaji kang padha sadawané norma partisi mau nyeraki nol. Yèn awaké dhéwé milih partisi P mbagi-bagi interval [0,b] dadi n subinterval kang ambané padha Δx = (b-0)/n = b/n lan titik t'i kang dipilih yaiku titik akir kiwa saben subinterval, partisi kang diéntuki awaké dhéwé yaiku:
- lan , saéngga:
Bebarengan karo n nyeraki ora kaétung lan norma partisi nyeraki 0, mula diéntuki:
Sajeroning praktèké, panrapan dhéfinisi integral tinentu nalika nggolèki pangaji integral tinentu mau arang banget digunakaké amarga ora praktis. Téoréma dhasar kalkulus (delengen pérangan ngisor) mènèhaké cara kang luwih praktis sajeroning panggolèkan pangaji integral tinentu.
Integral ora tentu[besut | besut sumber]
Nalika integral tinentu iku wilangan kang gedhéné ditemtokaké kanthi njupuk limit gunggungan Riemann, kang diasosiasikaké kanthi partisi interval katutup kang norma partisiné nyeraki nol, téoréma dhasar kalkulus (delengen pérangan ngisor) nélakaké yèn integral tinentu siji fungsi kontinu bisa diétung kanthi gampang yèn awaké dhéwé bisa golèk antiturunan/antiderivatif fungsi mau.
Yèn
Sakabèhing hmpunan antiturunan/antiderivatif siji fungsi ƒ iku integral ora tentu utawa uga primitif saka ƒ marang x lan ditulisaké kanthi matématis minangka:
Èksprèsi F(x) + C iku antiderivatif umum ƒ lan C iku konstanta sembarang.
Upamané ana siji fungsi , mula integral ora tentu utawa uga antiturunan saka fungsi mau yaiku:
Gateèkna yèn integral tinentu béda karo integral ora tentu. Integral tinentu sajeroning wangun iku wilangan, nalika integral ora tentu: iku fungsi kang duwé tambahan konstanta sembarang C.
Téoréma dhasar[besut | besut sumber]
Téoréma dhasar kalkulus nélakaké yèn turunan lan integral iku rong operasi kang silih adu arep. Luwih tepaté, téoréma iki nggandhèngaké pangaji saka anti derivatif karo integral tinentu. Amarga luwih gampang ngétung siji anti derivatif tinimbang nerapaké dhéfinisi integral tinentu, téoréma dhasar kalkulus mènèhi cara kang praktis sajeroning ngétung integral tinentu.
Téoréma dhasar kalkulus nélakaké:
Yèn siji fungsi f iku kontinu ing interval [a,b] lan yèn F iku fungsi kang ing ngendi turunané iku f ing interval (a,b), mula
Luwih lanjut, kanggo saben x ing interval (a,b),
Minangka contoné yèn awaké dhéwé arep ngétung pangaji integral , tinimbang migunakaké dhéfinisi integral tinentu minangka limit saka gunggung Riemann (delengen pérangan ndhuwur), awaké dhéwé bisa migunakaké téoréma dhasar kalkulus kanggo ngétung pangaji integral mau.
Anti derivatif saka fungsi iku . Mula saka iku, selaras karo téoréma dhasar kalkulus, pangaji saka integral tinentu yaiku:
Yèn awaké dhéwé arep golèk wiyar laladan A sangisoré kurva y=x ing interval [0,b], b>0, mula awaké dhéwé bakal éntuk:
Gatekna yèn asil kang diéntuk awaké dhéwé kanthi migunakaké téoréma dhasar kalkulus iki padha karo asil kang diéntuk kanthi nerapaké dhefinisi integral tinentu (delengen pérangan dhuwur). Amarga luwih praktis, téoréma dhasar kalkulus asring kanggo golèk pangaji integral tinentu.
Aplikasi[besut | besut sumber]

Kalkulus digunakaké ing saben cabang sains fisik, sains komputer, statistik, tèhnik, ékonomi, bisnis, kadhokteran, kapendhudhukan, lan ing babagan-babagan liyané. Saben konsèp ing mékanika klasik silih magepokan liwat kalkulus. Massa saka siji bandha karo massa jinis kang ora dikawruhi, momen inersia saka siji objèk, lan total ènèrgi saka siji objèk bisa ditemtokaké kanthi migunakaké kalkulus.
Sajeroning subdhisiplin listrik lan magnètisme, kalkulus bisa kanggo nggolèki total fluks saka siji médhan èlèktromagnètik. Conto historis liyané yaiku panggunaan kalkulus ing ukum obah Newton, ditélakaké minangka laju owah-owahan kang ngrujuk menyang turunan: Laju owah-owahan momèntum saka siji bandha yaiku padha karo résultan gaya kang makarya ing bandha mau kanthi arah kang padha.
Malah rumus umum saka ukum kaloro Newton: Gaya = Massa × Percepatan, migunakaké parumusan kalkulus difèrènsial amarga percepatan bisa ditélakaké minangka turunan saka karikatan. Téyori èlèktromagnètik Maxwell lan téyori rélativitas Einstein uga dirumusaké migunakaké kalkulus difèrènsial.
Réferènsi[besut | besut sumber]
Sumber[besut | besut sumber]
- ↑ Helmer Aslaksen. Why Calculus? National University of Singapore.
- ↑ Archimedes, Method, in The Works of Archimedes ISBN 978-0-521-66160-7
- ↑ Aryabhata the Elder
- ↑ Ian G. Pearce. Bhaskaracharya II. Archived 2016-09-01 at the Wayback Machine.
- ↑ Victor J. Katz (1995). "Ideas of Calculus in Islam and India", Mathematics Magazine 68 (3), pp. 163-174.
- ↑ J. L. Berggren (1990). "Innovation and Tradition in Sharaf al-Din al-Tusi's Muadalat", Journal of the American Oriental Society 110 (2), pp. 304-309.
- ↑ "Madhava". Biography of Madhava. School of Mathematics and Statistics University of St Andrews, Scotland. Dibukak ing 2006-09-13.
- ↑ "An overview of Indian mathematics". Indian Maths. School of Mathematics and Statistics University of St Andrews, Scotland. Dibukak ing 2006-07-07.
- ↑ "Science and technology in free India" (PDF). Government of Kerala — Kerala Call, September 2004. Prof.C.G.Ramachandran Nair. Diarsip saka sing asli (PDF) ing 2006-08-21. Dibukak ing 2006-07-09.
- ↑ Charles Whish (1835). Transactions of the Royal Asiatic Society of Great Britain and Ireland.
- ↑ UNESCO-World Data on Education isapi.dll?clientID=137079235&infobase=iwde.nfo&softpage=PL frame[pranala mati permanèn]
Pratélan pustaka[besut | besut sumber]
- Donald A. McQuarrie (2003). Mathematical Methods for Scientists and Engineers, University Science Books. ISBN 978-1-891389-24-5
- James Stewart (2002). Calculus: Early Transcendentals, 5th ed., Brooks Cole. ISBN 978-0-534-39321-2
Sumber liya[besut | besut sumber]
Wacan terusan[besut | besut sumber]
- Robert A. Adams. (1999) ISBN 978-0-201-39607-2 Calculus: A complete course.
- Albers, Donald J.; Richard D. Anderson and Don O. Loftsgaarden, ed. (1986) Undergraduate Programs in the Mathematics and Computer Sciences: The 1985-1986 Survey, Mathematical Association of America No. 7,
- John L. Bell: A Primer of Infinitesimal Analysis, Cambridge University Press, 1998. ISBN 978-0-521-62401-5.
- Florian Cajori, "The History of Notations of the Calculus." Annals of Mathematics, 2nd Ser., Vol. 25, No. 1 (Sep., 1923), pp. 1-46.
- Leonid P. Lebedev and Michael J. Cloud: "Approximating Perfection: a Mathematician's Journey into the World of Mechanics, Ch. 1: The Tools of Calculus", Princeton Univ. Press, 2004
- Cliff Pickover. (2003) ISBN 978-0-471-26987-8 Calculus and Pizza: A Math Cookbook for the Hungry Mind.
- Michael Spivak. (Sept 1994) ISBN 978-0-914098-89-8 Calculus. Publish or Perish publishing.
- Silvanus P. Thompson dan Martin Gardner. (1998) ISBN 978-0-312-18548-0 Calculus Made Easy.
- Mathematical Association of America. (1988) Calculus for a New Century; A Pump, Not a Filter, The Association, Stony Brook, NY. ED 300 252.
- Thomas/Finney. (1996) ISBN 978-0-201-53174-9 Calculus and Analytic geometry 9th, Addison Wesley.
- Weisstein, Eric W. "Second Fundamental Theorem of Calculus." dari MathWorld—A Wolfram Web Resource.
Pustaka daring[besut | besut sumber]
- Crowell, B., (2003). "Calculus" Light and Matter, Fullerton. Retrieved 6th May 2007 from http://www.lightandmatter.com/calc/calc.pdf
- Garrett, P., (2006). "Notes on first year calculus" University of Minnesota. Retrieved 6th May 2007 from http://www.math.umn.edu/~garrett/calculus/first_year/notes.pdf
- Faraz, H., (2006). "Understanding Calculus" Retrieved Retrieved 6th May 2007 from Understanding Calculus, URL http://www.understandingcalculus.com/ (HTML only)
- Keisler, H. J., (2000). "Elementary Calculus: An Approach Using Infinitesimals" Retrieved 6th May 2007 from http://www.math.wisc.edu/~keisler/keislercalc1.pdf
- Mauch, S. (2004). "Sean's Applied Math Book" California Institute of Technology. Retrieved 6th May 2007 from http://www.cacr.caltech.edu/~sean/applied_math.pdf Archived 2007-06-14 at the Wayback Machine.
- Sloughter, Dan., (2000) "Difference Equations to Differential Equations: An introduction to calculus". Retrieved 6th May 2007 from http://math.furman.edu/~dcs/book/
- Stroyan, K.D., (2004). "A brief introduction to infinitesimal calculus" University of Iowa. Retrieved 6th May 2007 from http://www.math.uiowa.edu/~stroyan/InfsmlCalculus/InfsmlCalc.htm (HTML only)
- Strang, G. (1991) "Calculus" Massachusetts Institute of Technology. Retrieved 6th May 2007 from http://ocw.mit.edu/ans7870/resources/Strang/strangtext.htm.
Kaca wèb[besut | besut sumber]
- Calculus.org: The Calculus page di Universitas California, Davis
- COW: Calculus on the Web di Universitas Temple
- Online Integrator (WebMathematica) dari Wolfram Research
- The Role of Calculus in College Mathematics Archived 2021-07-26 at the Wayback Machine. dari ERICDigests.org
- OpenCourseWare Calculus dari Institut Teknologi Massachusetts
- Infinitesimal Calculus Encyclopaedia of Mathematics, Michiel Hazewinkel ed..
| Artikel iki minangka artikel rintisan. Kowé bisa ngéwangi Wikipédia ngembangaké. |



















![{\displaystyle [x_{0},x_{1}],[x_{1},x_{2}],\ldots ,[x_{n-1},x_{n}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e6e703c312490f26ff6dd5e474f67c6606b57b6c)

























